geometri ruang | Olimpiade Matematika

Posts Tagged ‘geometri ruang’

Kanada 1983 #3

3. Luas segitiga ditentukan oleh panjang sisi-sisinya. Apakah volume tetrahedron ditentukan oleh luas sisi-sisinya?

Solusi:

Tidak. Misalkan $S$ adalah segitiga sama sisi dan $T$ adalah segitiga yang sudutnya mendekati $90^{\circ}$ dan sama kaki, keduanya memiliki luas 4. Pada kedua segitiga, buat garis yang menghubungkan titik-titik tengah sisi-sisinya. Lipat kedua segitiga sepanjang garis-garis tersebut, maka pada masing-masing $S$ dan $T$ didapat empat segitiga dengan luas 1. Perhatikan bahwa $S$ menjadi tetrahedron beraturan dengan volume positif. Tetapi $T$ menjadi tetrahedron yang volumenya mendekati 0. Semakin dekat sudutnya dengan $90^{\circ}$ , volumenya semakin kecil. Jadi dua tetrahedron ini memiliki luas sisi-sisi yang sama tetapi volumenya berbeda, sehingga bukti kita selesai.

Written by olimpiadematematika

25 Juni 2009 at 19:51

Ditulis dalam olimpiade matematika

Tagged with geometri, geometri ruang, kanada, olimpiade matematika, segitiga, tetrahedron, volume

Kanada 1982 #5

5. Garis-garis tinggi dari tetrahedron $ABCD$ diperpanjang keluar sampai titik $A',B',C',D'$ berturut-turut, di mana $AA'=k/h_a$ , $BB'=k/_b$ , $CC'=k/h_c$ dan $DD'=k/h_d$ . Di sini, $k$ konstan dan $h_a$ menyatakan panjang garis tinggi $ABCD$ dari titik $A$ , dan sebagainya. Buktikan bahwa titik berat dari tetrahedron $A'B'C'D'$ berimpit dengan titik berat $ABCD$ .

Solusi:

Buat sistem koordinat dengan pusat $O$ sebagai titik berat $ABCD$ . Maka $\overrightarrow{A}+\overrightarrow{B}+\overrightarrow{C}+\overrightarrow{D}=\overrightarrow{O}$ . Kita perlu menunjukkan $\overrightarrow{A'}+\overrightarrow{B'}+\overrightarrow{C'}+\overrightarrow{D'}=0$ atau $\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}+\overrightarrow{DD'}=\overrightarrow{O}$ . Perhatikan vektor $\overrightarrow{BD}\times\overrightarrow{CD}=(\overrightarrow{D}-\overrightarrow{B})\times(\overrightarrow{D}-\overrightarrow{C})=\overrightarrow{B}\times\overrightarrow{C}+\overrightarrow{C}\times\overrightarrow{D}+\overrightarrow{D}\times\overrightarrow{B}$ . Vektor ini tegak lurus $BCD$ , maka sejajar terhadap $\overrightarrow{AA'}$ . Besarnya adalah $2\times[BCD]$ yaitu $6V/h_a$ di mana $V$ adalah volume $ACD$ . Maka $\overrightarrow{AA'}=\frac{k}{6V}(\overrightarrow{B}\times\overrightarrow{C}+\overrightarrow{C}\times\overrightarrow{D}+\overrightarrow{D}\times\overrightarrow{B})$ . Bentuk serupa bisa didapat untuk $\overrightarrow{BB'},\overrightarrow{CC'},\overrightarrow{DD'}$ . Maka $\frac{6V}k(\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}+\overrightarrow{DD'})=\sum(\overrightarrow{B}\times\overrightarrow{C}+\overrightarrow{C}\times\overrightarrow{D}+\overrightarrow{D}\times\overrightarrow{B})=\overrightarrow{O}$ . Jadi titik berat dari $A'B'C'D'$ juga di $O$ .

Written by olimpiadematematika

5 Juni 2009 at 19:01

Ditulis dalam olimpiade matematika

Tagged with garis tinggi, geometri, geometri ruang, olimpiade matematika, tetrahedron, vektor

Solusi AIME 1983

1. Perhatikan bahwa $\log_wx=\frac1{24}$ , $\log_wy=\frac1{40}$ dan $\log_w{xyz}=\frac1{12}$ , maka $\log_wz=\frac1{12}-\frac1{40}-\frac1{24}=\frac1{60}$ , jadi $\log_zw=60$ .

2. $f(x)=(x-p)+(15-x)+(p+15-x)=30-x\ge30-15=15$ .

3. Misalkan $x^2+18x+30=y$ , maka $y=2\sqrt{y+15}$ . Kuadratkan, didapat $y^2=4y+60$ atau $y^2-4y-60=0$ , $(y+6)(y-10)=0$ , maka $y=-6$ atau $y=10$ . Jika $x^2+18x+30=-6$ , maka $x^2+18x+36=0$ yang memiliki dua akar real dengan hasil kali 36. Jika $x^2+18x+30=10$ , maka $x^2+18x+20=0$ yang memiliki dua akar real lagi dengan hasil kali 20. Jadi hasil kali semua akarnya adalah 720.

4. Perhatikan gambar. Misalkan $OE=x,OD=y$ . Maka $OA^2=OD^2+AD^2$ dan $OC^2=EC^2+EO^2$ , sehingga $50=y^2+(6-x)^2=x^2+(y+2)^2$ . Selesaikan ini, didapat $x=1,y=5$ , maka $OB^2=1^2+5^2=26$ .

5. Misalkan $x+y=a$ , maka $xy=\frac{a^2-7}2$ . Dari $x^3+y^3=(x+y)(x^2-xy+y^2)$ , substitusikan nilai-nilai yang kita ketahui, didapat $(a-1)(a-4)(a+5)=0$ , maka nilai maksimumnya 4.

6. Perhatikan bahwa $a_{83}=6^{83}+8^{83}=(7-1)^{83}+(7+1)^{83}$ . Uraikan dengan binomium Newton, maka didapat modulo 49-nya adalah $\binom{83}17-1+\binom{83}17+1\equiv35\pmod{49}$ .

7. Banyaknya cara memilih tiga prajurit adalah $\binom{25}3$ . Banyaknya cara memilih tiga orang yang berurutan adalah 25, banyaknya cara memilih tiga orang sehingga hanya dua yang bersebelahan adalah $25\times 21$ (pilih dua orang bersebelahan dulu kemudian pilih orang ketiga yang tidak bersebelahan dengan kedua orang itu). Maka peluangnya adalah $\frac{25+25\times21}{\binom{25}3}=\frac{11}{46}$ . Jawabannya 11+46=57.

8. Perhatikan bahwa $\binom{200}{100}=\frac{101\cdot102\cdots200}{1\cdot2\cdots100}$ . Penyebutnya mengandung semua bilangan prima dua digit, maka faktor prima itu harus muncul minimal dua kali di $101\cdot102\cdots200$ . Jadi $3p\le200$ , $p\le66$ . Bilangan prima terbesar yang memenuhi ini adalah 61, dan mudah dicek bahwa 61 muncul dua kali di pembilang dan satu kali di penyebut.

9. Gunakan ketaksamaan AM-GM, $\frac{9x^2\sin^2x+4}{x\sin x}=9x\sin x+\frac4{x\sin x}\ge12$ . Kesamaan terjadi ketika $9x\sin x=\frac4{x\sin x}$ , yaitu $x\sin x=\frac23$ . Tetapi $x\sin x$ adalah fungsi kontinu pada interval $[0,\pi/2]$ , maka nilai tersebut pasti bisa tercapai.

10. Ada beberapa kemungkinan nilai seperti berikut (setiap huruf mewakili angka yang berbeda-beda): 11ab, 1a1b, 1ab1, 1aab, 1aba, 1baa. Banyaknya bilangan ini adalah $6\times(9\times8)=432$ .

11. Mudah dilihat bahwa tinggi bangun tersebut adalah 6. Perhatikan gambar di bawah. Kita lengkapi bangun tersebut menjadi prisma segitiga yang volume $\frac{6\sqrt2\cdot12\sqrt2\cdot6}2=432$ . Kita kurangi ini dengan volume dua piramida tambahan yang luasnya $2\times\frac{6\sqrt2\cdot3\sqrt2\cdot6}3=144$ . Jadi volume bangun yang kita cari adalah $432-144=288$ .

12. Misalkan $AB=10a+b,CD=10b+a$ . Maka $CO=\frac{10a+b}2$ dan $CH=\frac{10b+a}2$ , maka $HO=\sqrt{\left(\frac{10a+b}2\right)^2-\left(\frac{10b+a}2\right)^2}=\frac32\sqrt{11(a+b)(a-b)}$ . Maka bisa didapat $a+b=11,a-b=1$ , sehingga $a=6,b=5$ . Jadi $AB=65$ .

13. Jika $S$ adalah himpunan bagian tak kosong dan $\{1,2,3,4,5,6\}$ , jumlah bolak-balik dari $S$ dengan jumlah bolak-balik dari $S\cup\{7\}$ adalah 7. Karena ada $2^6-1=63$ pasang seperti ini, maka jumlah semuanya adalah $63\times7=441$ . Tapi masih ada satu himpunan bagian yang belum dihitung yaitu {7} yang jumlahnya 7. Jadi jawabannya 448.

14. $A,B$ diproyeksikan ke $RQ$ sampai di $C,D$ berturut-turut. Titik $B$ diproyeksikan ke $AC$ di titik $K$ . Misalkan $AB$ memotong lingkaran besar dan kecil di $M,N$ berturut-turut. Perhatikan bahwa $BKA$ adalah segitiga siku-siku dan $AM=MB$ , maka $KM$ adalah garis berat sehingga $KM=6$ . Misalkan $PR=x$ . Perhatikan bahwa $KBA$ dan $CRA$ adalah dua segitiga sebangun dengan perbandingan panjang $3:2$ . Maka $CA=\sqrt{AR^2-CR^2}=\sqrt{AP^2-CP^2}$ . Substitusikan $AR=18,CR=\frac32x,CP=x,AP=8$ , didapat $x^2=130$ .

15. Misalkan $A$ adalah titik tetap dan $D$ bergerak sepanjang lingkaran. Misalkan juga $N$ adalah titik tengah dari tali busur $AD$ . Perhatikan bahwa titik $N$ bergerak di sepanjang lingkaran di mana $AO$ adalah diameternya, anggaplah pusat lingkaran ini adalah $P$ . Titik $N$ bisa memotong $BC$ di nol, satu, atau dua titik. Menurut pernyataan soal, hanya ada satu titik $N$ di $BC$ , maka lingkaran $P$ menyinggung garis $BC$ . Perhatikan bahwa $BO=5,BM=3$ , maka $MO=4$ dan $\tan BOM=\frac34$ . Perhatikan juga bahwa $MO=PN+PO\cos\angle AOM=\frac52+\frac52\cos\angle AOM=4$ , maka $\cos\angle AOM=\frac35$ . Jadi $\tan \angle AOB=\frac{\tan\angle AOM-\tan\angle BOM}{1+\tan\angle AOM\tan\angle BOM}=\frac7{24}$ . Jadi $\sin AOM=\frac7{25}$ dan jawabannya $7\cdot25=175$ .

Written by olimpiadematematika

24 Mei 2009 at 13:14

Ditulis dalam olimpiade matematika

Tagged with aime 1983, aljabar, binomium, fungsi, fungsi kontinu, geometri, geometri euklid, geometri ruang, himpunan, kombinasi, kombinatorika, logaritma, modulus, newton, nilai mutlak, persamaan kuadrat, probabilitas, proyeksi, solusi, teori bilangan, volume

Kanada 1980 #5

5. Sebuah balok memiliki sifat bahwa penampang yang sejajar dengan satu sisi $F$ memiliki keliling yang sama dengan $F$ . Tentukan apakah ada polihedron lain yang memiliki sifat tersebut.

Solusi:

Oktahedron beraturan juga memiliki sifat ini. Misalkan panjang rusuknya $l$ . Mudah dilihat bahwa penampang yang sejajar dengan sisinya adalah segienam dengan panjang sisi berturut-turut $x,y,x,y,x,y$ dengan $x+y=l$ . Maka kelilingnya sama dengan keliling sisinya.

Written by olimpiadematematika

20 Mei 2009 at 21:59

Ditulis dalam olimpiade matematika

Tagged with balok, geometri ruang, keliling, matematika, oktahedron, olimpiade, polihedron

Kanada 1979 #2

2. Dalam geometri Euklidean, jumlah sudut dalam segitiga selalu konstan. Tetapi, buktikan bahwa jumlah sudut dihedral dari sebuah tetrahedron tidak konstan.

Solusi:

Tinjau sebuah tetrahedron dengan alas segitiga sama sisi dan titik puncaknya $P$ berada tepat di atas pusat alasnya $G$ . Jika sudut dihedral yang dibentuk di alas adalah $\alpha$ dan sudut yang dibentuk sisi lainnya adalah $\beta$ , maka jumlah sudutnya adalah $3(\alpha+\beta)$ . Jika $G$ mendekati $G$ , maka $\alpha$ mendekati 0 dan $\beta$ mendekati $\pi$ . Jadi jumlah sudutnya bisa mendekati $3\pi$ . Jika $P$ menjauhi $P$ menjauhi $G$ , $\alpha,\beta$ masing-masing mendekati $\frac{\pi}2$ . Jadi jumlahnya bisa mendekati $3\pi/2$ . Ini menunjukkan jumlah sudutnya tidak konstan.

Written by olimpiadematematika

20 Mei 2009 at 18:43

Ditulis dalam olimpiade matematika

Tagged with geometri euklidean, geometri ruang, olimpiade matematika, sudut dihedral, tetrahedron

Kanada 1977 #5

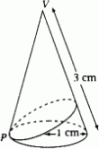
5. Suatu kerucut memiliki radius alas 1 cm dan tinggi kemiringannya 3 cm. Titik $P$ adalah titik pada keliling alas dan dibuat jalan terpendek mengelilingi kerucut sampai kembali ke $P$ . Tentukan jarak terpendek dari puncak $V$ ke jalan ini.

Solusi:

Kita buka kerucut ini dengan memotong $VP$ . Didapat sektor lingkaran dengan jari-jari 3 dan panjang busur $2\pi$ . Jalan terpendek mengelilingi kerucut sama dengan panjang busur $P_1P_2$ pada sektor itu, dan jarak jalan ini ke $V$ sama dengan panjang $h=VA$ seperti gambar di bawah. Tetapi kita punya $\frac{2\theta}{2\pi}=\frac{2\pi}{2\pi\cdot3}$ , atau $\theta=\pi/3$ . Jadi $\frac{h}3=\cos(\pi/3)$ , sehingga $h=\frac32$ .

Written by olimpiadematematika

13 Mei 2009 at 7:09

Ditulis dalam olimpiade matematika

Tagged with busur, geometri ruang, kerucut, sektor lingkaran

Kanada 1976 #6

6. Jika $A,B,C,D$ adalah empat titik pada ruang sehingga $\angle ABC=\angle BCD=\angle CDA=\angle DAB=90^{\circ}$ , buktikan $A,B,C,D$ koplanar.

Solusi:

Misalkan $B(0,0,0),C(0,y,0),A(x,0,0),D(u,v,w)$ . Karena $\angle BAD=90^{\circ}$ , maka $u=x$ . Kemudian $\angle BCD=90^{\circ}$ , maka $v=y$ . Dari $\angle CDA=90^{\circ}$ , maka

$x^2+y^2=AC^2=AD^2+DC^2=((x-u)^2+v^2+w^2)+(u^2+(v-y)^2+w^2)=y^2+w^2+x^2+w^2$

jadi $w=0$ .

Written by olimpiadematematika

11 Mei 2009 at 21:42

Ditulis dalam olimpiade matematika

Tagged with geometri ruang, koordinat cartesius, koplanar, tegak lurus

IMO 1967 #2

2. Suatu tetrahedron memiliki satu dan hanya satu rusuk yang panjangnya lebih besar dari 1. Buktikan bahwa volumenya tidak lebih besar dari 1/8.

Solusi:

Tanpa mengurangi keumuman, anggaplah $CD$ adalah rusuk terpanjang dari tetrahedron $ABCD$ . Misalkan $AB=x$ .

Ambil titik $T$ pada $AB$ sehingga $CT$ adalah garis tinggi, anggaplah $T$ lebih dekat ke $A$ daripada ke $B$ . Jadi $BT\ge\frac{x}2$ dan $CT=\sqrt{CB^2-BT^2}\le\sqrt{1-\frac{x^2}4}$ .

Dengan cara yang serupa, garis tinggi segitiga $ABD$ dari titik $D$ memiliki panjang $m_1\le\sqrt{1-\frac{x^2}4}$ .

Garis tinggi tetrahedron tersebut dari titik $C$ memiliki panjang tidak lebih dari $CT$ , $m\le\sqrt{1-\frac{x^2}4}$ .

Jadi volume tetrahedron tersebut adalah $\frac13\left(\frac12AB\cdot m_1\right)\cdot m=\frac{x}{6}\left(1-\frac{x^2}4\right)$ . Kita ingin membuktikan ini tidak lebih dari 1/8, yang ekuivalen dengan $(x-1)(x^2+x-3)\ge0$ . Ini pasti benar karena $0<x\le 1$ .

Written by olimpiadematematika

3 Mei 2009 at 8:16

Ditulis dalam olimpiade matematika

Tagged with aljabar, garis tinggi, geometri ruang, IMO 1967, ketaksamaan, matematika, olimpiade, rusuk, tetrahedron, volume

IMO 1966 #3

3. Buktikan bahwa jumlah jarak dari titik-titik sudut sebuah tetrahedron beraturan dan pusatnya lebih kecil dari jumlah jarak titik-titik tersebut ke titik lain manapun pada ruang.

Solusi:

Misalkan titik-titik sudutnya adalah $A(-a,-a,-a),B(-a,a,a),C(a,-a,a),D(a,a,-a)$ . Titik pusatnya adalah $O(0,0,0)$ . Misalkan terdapat sebarang titik $X(x,y,z)$ dengan $X\ne O$ . Dengan ketaksamaan AM-QM,

$XA+XB+XC+XD\le2\sqrt{XA^2+XB^2+XC^2+XD^2}=4\sqrt{(x^2+y^2+z^2)+3a^2}<4a\sqrt3=OA+OB+OC+OD$

Maka kita selesai.

Written by olimpiadematematika

24 April 2009 at 10:20

Ditulis dalam olimpiade matematika

Tagged with geometri ruang, imo 1966, ketaksamaan AM-QM, koordinat kartesius, olimpiade matematika sma, tetrahedron

IMO 1965 #3

3. Diberikan tetrahedron $ABCD$ . Tetrahedron tersebut dibagi menjadi dua bagian oleh bidang $\pi$ yang sejajar terhadap $AB$ dan $CD$ . Hitunglah rasio volume dari kedua bagian jika rasio jarak dari $\pi$ ke $AB$ terhadap jaraknya ke $CD$ adalah $k$ .

Solusi:

Misalkan $E\in AC, F\in BC, G\in BD, H\in AD$ sehingga $EFGH$ adalah penampang bidang $\pi$ . Misalkan juga $X\in AB$ adalah titik sehingga $HX\parallel DB$ . Jelas bahwa $V_{AEHBFG}=V_{AXEH}+V_{XEHBFG}$ . Misalkan $MN$ adalah garis yang tegak lurus terhadap garis $AB$ dan $CD$ ( $M\in AB, N\in CD$ ) dan misalkan $MN,BN$ memotong bidang $\pi$ pada $Q,R$ berturut-turut. Maka jelas bahwa $BR/RN=MQ/QN=k$ , sehingga $AX/XB=AE/EC=AH/HD=BF/FC=BG/GD=k$ . Jadi $V_{AXEH}/V_{ABCD}=k^3/(k+1)^3$ . Jika $h=3V_{ABCD}/L_{ABC}$ adalah tinggi tetrahedron $ABCD$ dari titik $D$ , maka $V_{XEHBFG}=\frac12L_{XBFE}\frac{k}{k+1}h$ dan $\frac{L_{XBFE}}{L_{ABC}}=\frac{L_{ABC}-L_{AXE}-L_{EFC}}{L_{ABC}}=\frac{(k+1)^2-1-k^2}{(k+1)^2}=\frac{2k}{(1+k)^2}$ . Maka kita punya $V_{XEHBFG}/V_{ABCD}=3k^2/(1+k)^3$ , dan $V_{A E H B F G}/V_{A B C D}=(k^3+3k^2)/(k+1)^3$ . Maka kita juga dapat $V_{CEFDHG}/V_{ABCD}=(3k+1)/(k+1)^3$ , sehingga rasio yang dicari adalah $(k^3+3k^2)/(3k+1)$ .